（桂林）如图，四边形ABCD是⊙O的内接正方形，AB4，PC

首页 / 初中数学 / 试题详细

更新 2022-09-03
科目数学
题型解答题
难度中等
浏览 609

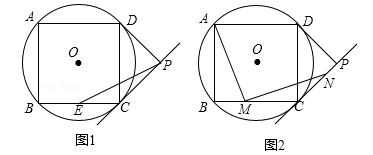
（桂林）如图，四边形ABCD是⊙O的内接正方形，AB=4，PC、PD是⊙O的两条切线，C、D为切点．
（1）如图1，求⊙O的半径；
（2）如图1，若点E是BC的中点，连接PE，求PE的长度；
（3）如图2，若点M是BC边上任意一点（不含B、C），以点M为直角顶点，在BC的上方作∠AMN=90°，交直线CP于点N，求证：AM=MN．

登录免费查看答案和解析

相关试题

勤劳是中华民族的传统美德，学校要求学们在家帮助父母做一些力所能及的家务．在学期初，小丽同学随机调查了七年级部分同学寒假在家做家务的总时间，设被调查的每位同学寒假在家做家务的总时间为x小时，将做家务的总时间分为五个类别： $A （ 0 \leq x ＜ 10 ）$ ， $B （ 10 \leq x ＜ 20 ）$ ， $C （ 20 \leq x ＜ 30 ）$ ， $D （ 30 \leq x ＜ 40 ）$ ， $E （ x \geq 40 ）$ ．并将调查结果绘制了如图两幅不完整的统计图：

根据统计图提供的作息，解答下列问题：

（1）本次共调查了　　名学生；

（2）根据以上信息直接在答题卡上补全条形统计图；

（3）扇形統计图中m＝　　，类别D所对应的扇形圆心角α的度数是　　度；

（4）若该校七年级共有400名学生，根据抽样调查的结果，估计该校七年級有多少名学生寒假在家做家务的总时间不低于20小时？

题型：未知
难度：未知

收藏答案/解析

古希腊数学家毕达哥拉斯认为：“一切平面图形中最美的圆”，请研究如下美丽的圆，如图， $Rt △ ABC$ 中， $∠ BCA ＝ 90 °$ ， $AC ＝ 3$ ， $BC ＝ 4$ ，点O在线段 $BC$ 上，且 $OC = \frac{3}{2}$ ，以O为圆心． $OC$ 为半径的 $⊙ O$ 交线段AO于点D，交线段AO的延长线于点E．

（1）求证： $AB$ 是 $⊙ O$ 的切线；

（2）研究过短中，小明同学发现 $\frac{AC}{AE} = \frac{AD}{AC}$ ，回答小明同学发现的结论是否正确？如果正确，给出证明；如果不正确，说明理由．

题型：未知
难度：未知

收藏答案/解析

（1）计算 ${(- \frac{1}{2})}^{- 1} - 3 \tan 60 ° + |- \sqrt{3}| + {(2 \cos 60 ° - 2020)}^{0}$ ；

（2）解不等式组： $\{\begin{matrix} \frac{3 - x}{2} \leq 1 \\ 3 x + 2 \geq 4 \end{matrix}$ ．

题型：未知
难度：未知

收藏答案/解析

如图，二次函数 $y ＝ \frac{1}{4} x^{2} + bx + c$ 的图象过点 $A （ 4 ，﹣ 4 ）$ ， $B （﹣ 2 ， m ）$ ，交y轴于点 $C （ 0 ，﹣ 4 ）$ ．直线BO与抛物线相交于另一点D，连接 $AB ， AD$ ，点E是线段AB上的一动点，过点E作 $EF ∥ BD$ 交AD于点F．

（1）求二次函数 $y ＝ \frac{1}{4} x^{2} + bx + c$ 的表达式；

（2）判断 $△ AB D$ 的形状，并说明理由；

（3）在点E的运动过程中，直线 $BD$ 上存在一点G，使得四边形AFGE为矩形，请判断此时 $AG 与 BD$ 的数量关系，并求出点E的坐标；

（4）点H是抛物线的顶点，在（3）的条件下，点P是平面内使得 $∠ EPF ＝ 90 °$ 的点，在抛物线的对称轴上，是否存在点Q，使得 $△ HPQ$ 是以 $∠ PQH$ 为直角的等腰直角三角形，若存在，直接写出符合条件的所有点Q的坐标；若不存在，请说明理由．

题型：未知
难度：未知

收藏答案/解析

如图，在 $▱ ABCD$ 中， $DE ⊥ AC$ 于点O，交BC于点E， $EG ＝ EC$ ， $GF ∥ AD$ 交DE于点F，连接 $FC$ ，点H为线段 $AO$ 上一点，连接 $HD ， HF$ ．

（1）判断四边形 $GECF$ 的形状，并说明理由；

（2）当 $∠ DHF ＝ ∠ HAD$ 时，求证： $AH • CH ＝ EC • AD$ ．

题型：未知
难度：未知

收藏答案/解析

推荐套卷

热门套卷