如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，点D以每秒1个单位长度的速度由点A向点B匀速运动，到达B点即停止运动，M，N分别是AD，CD的中点，连接MN，设点D运动的时间为t．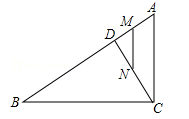
（1）判断MN与AC的位置关系；
（2）求点D由点A向点B匀速运动的过程中，线段MN所扫过区域的面积；
（3）若△DMN是等腰三角形，求t的值．
相关试题
已知一个角的两边与另一个角的两边分别平行，结合下图，试探索这两个角之间的数量关系，并说明你的理由.
（1）如图1，AB∥EF，BC∥DE.猜想∠1与∠2的数量关系是：_______.
（2）如图2，AB∥EF，BC∥DE. 猜想∠1与∠2的数量关系是：_______.
（3）由（1）（2）可以得出的结论是：如果一个角的两边与另一个角的两边分别平行，那么这两个角_____ .
粤公网安备 44130202000953号