（·湖南株洲）“皮克定理”是来计算原点在整点的多边形面积的公式，公式表达式为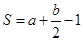
，孔明只记得公式中的S表示多边形的面积，
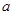和
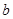中有一个表示多边形那边上（含原点）的整点个数，另一个表示多边形内部的整点的个数，但不记得究竟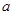是还是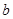表示多边形内部的整点的个数，请你选择一些特殊的多边形（如图1）进行验证，得到公式中表示多边形内部整点个数的字母是 ；并运用这个公式求得如图2中多边形的面积是 ．
相关试题
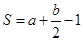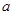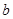（·湖南株洲）“皮克定理”是来计算原点在整点的多边形面积的公式，公式表达式为，孔明只记得公式中的S表示多边形的面积，和中有一个表示多边形那边上（含原点）的整点个数，另一个表示多边形内部的整点的个数，但不记得究竟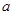是还是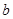表示多边形内部的整点的个数，请你选择一些特殊的多边形（如图1）进行验证，得到公式中表示多边形内部整点个数的字母是 ；并运用这个公式求得如图2中多边形的面积是 ．
等于．
粤公网安备 44130202000953号