（攀枝花）如图，在菱形ABCD中，AB=BD，点E、F分别是AB、AD上任意的点（不与端点重合），且AE=DF，连接BF与DE相交于点G，连接CG与BD相交于点H．给出如下几个结论：①△AED≌△DFB；②S四边形BCDG=
；③若AF=2DF，则BG=6GF；④CG与BD一定不垂直；⑤∠BGE的大小为定值．
其中正确的结论个数为（ ）
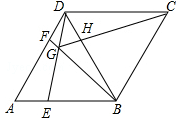
A．4 B．3 C．2 D．1
相关试题
（攀枝花）如图，在菱形ABCD中，AB=BD，点E、F分别是AB、AD上任意的点（不与端点重合），且AE=DF，连接BF与DE相交于点G，连接CG与BD相交于点H．给出如下几个结论：①△AED≌△DFB；②S四边形BCDG=；③若AF=2DF，则BG=6GF；④CG与BD一定不垂直；⑤∠BGE的大小为定值．
其中正确的结论个数为（ ）
A．4 B．3 C．2 D．1
绕点
逆时针旋转
到
的位置，已知
，则
等于（）
粤公网安备 44130202000953号