（遂宁）下列命题：①对角线互相垂直的四边形是菱形；
②点G是△ABC的重心，若中线AD=6，则AG=3；
③若直线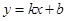
经过第一、二、四象限，则k＜0，b＞0；
④定义新运算：a*b=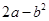
，若（2x）*（x﹣3）=0，则x=1或9；
⑤抛物线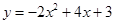
的顶点坐标是（1，1）．
其中是真命题的有 （只填序号）
相关试题
（遂宁）下列命题：①对角线互相垂直的四边形是菱形；
②点G是△ABC的重心，若中线AD=6，则AG=3；
③若直线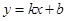经过第一、二、四象限，则k＜0，b＞0；
④定义新运算：a*b=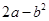，若（2x）*（x﹣3）=0，则x=1或9；
⑤抛物线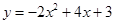的顶点坐标是（1，1）．
其中是真命题的有 （只填序号）
是方程
的两实数根，则
的值为。
粤公网安备 44130202000953号