某校学生会决定从三名学生会干事中选拔一名干事，对甲、乙、丙三名候选人进行了笔试和面试，三人的测试成绩如下表所示：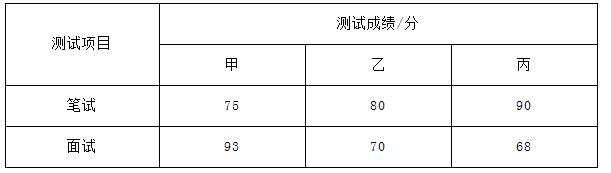
根据录用程序，学校组织200名学生采用投票推荐的方式，对三人进行民主测评，三人得票率（没有弃权，每位同学只能推荐1人）如扇形统计图所示，每得一票记1分．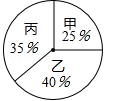
（1）分别计算三人民主评议的得分；
（2）根据实际需要，学校将笔试、面试、民主评议三项得分按4：3：3的比例确定个人成绩，三人中谁的得分最高？
相关试题
为直线
上一点, 过点
、
、
，且
，
，
，求：
的度数.
（1）如图所示，∠AOB=90°，∠BOC=30°，OM平分∠AOC，ON平分∠BOC，求∠MON的度数．
（2）如果（1）中∠AOB=α，其他条件不变，求∠MON的度数．
（3）如果（1）中∠BOC=β（β为锐角），其他条件不变，求∠MON的度数．
（4）从（1）（2）（3）的结果你能看出什么规律？
（5）线段的计算与角的计算存在着紧密的联系，它们之间可以互相借鉴解法，请你模仿（1）～（4），设计一道以线段为背景的计算题，并写出其中的规律来？
粤公网安备 44130202000953号