（乐山）在直角坐标系xOy中，对于点P（x，y）和Q（x，y′），给出如下定义：若
，则称点Q为点P的“可控变点”．
例如：点（1，2）的“可控变点”为点（1，2），点（﹣1，3）的“可控变点”为点（﹣1，﹣3）．
（1）若点（﹣1，﹣2）是一次函数
图象上点M的“可控变点”，则点M的坐标为 ；
（2）若点P在函数
（
）的图象上，其“可控变点”Q的纵坐标y′的取值范围是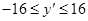
，则实数a的取值范围是 ．
（乐山）在直角坐标系xOy中，对于点P（x，y）和Q（x，y′），给出如下定义：若，则称点Q为点P的“可控变点”．
例如：点（1，2）的“可控变点”为点（1，2），点（﹣1，3）的“可控变点”为点（﹣1，﹣3）．
（1）若点（﹣1，﹣2）是一次函数图象上点M的“可控变点”，则点M的坐标为 ；
（2）若点P在函数（）的图象上，其“可控变点”Q的纵坐标y′的取值范围是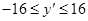，则实数a的取值范围是 ．
－12ab+12a= .
有意义．
的解是_______________
粤公网安备 44130202000953号