（本小题满分6分）
某小学为了解学生每天完成家庭作业所用时间的情况，从每班抽取相同数量的学生进行调查，并将所得数据进行整理，制成条形统计图和扇形统计图如下：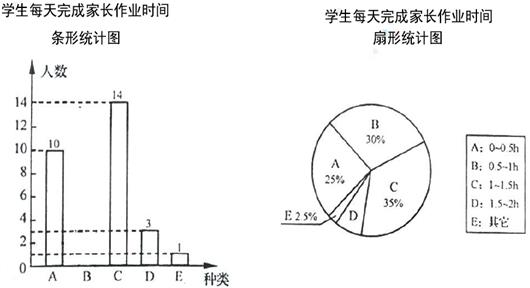
（1）补全条形统计图；
（2）求扇形统计图中扇形D的圆心角的度数；
（3）若该中学有2000名学生，请估计其中有多少名学生能在1．5小时内完成家庭作业？
相关试题
如图，△ABC在坐标平面内三个顶点的坐标分别为A（1，2）、B（3，3）、
C（3，1）．
（1）根据题意，请你在图中画出△ABC；
（2）在原图中,以B为位似中心，画出△A′BC′使它与△ABC位似且位似比是3：1，并写出顶点A′和C′的坐标．
如图，从A地到B地的公路需经过C地，图中AC=10千米，∠CAB=25°，∠CBA=37°，因城市规划的需要，将在A、B两地之间修建一条笔直的公路．
（1）求改直的公路AB的长（精确到0．1）；
（2）问公路改直后比原来缩短了多少千米（精确到0．1）？
、
、
，且
．
的值．
，求
粤公网安备 44130202000953号