已知某船顺水航行3小时,逆水航行2小时,
(1)已知轮船在静水中前进的速度是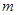 千米/时,水流的速度是a千米/时,则轮船共航行多少千米?
千米/时,水流的速度是a千米/时,则轮船共航行多少千米?
(2)轮船在静水中前进的速度是80千米/时,水流的速度是3千米/时,则轮船共航行多少千米?
相关知识点
推荐套卷
已知某船顺水航行3小时,逆水航行2小时,
(1)已知轮船在静水中前进的速度是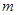 千米/时,水流的速度是a千米/时,则轮船共航行多少千米?
千米/时,水流的速度是a千米/时,则轮船共航行多少千米?
(2)轮船在静水中前进的速度是80千米/时,水流的速度是3千米/时,则轮船共航行多少千米?