探索思考：伟大的数学家高斯在上学读书时曾经研究过这样一个问题：1+2+3+…+10=？
经过研究，这个问题的一般性结论是：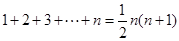
,其中n是正整数。现在，我们来研究一个类似的问题：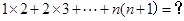
观察下面三个特殊的等式：
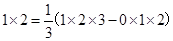
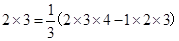
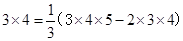
将这三个等式的两边相加，可以得到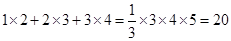
。
读完这段材料，请你计算下列各题：
（1）
；
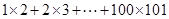（2）
；
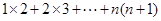（3）
．
，其中x=﹣1．
；
；
≤
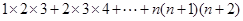相关知识点
推荐套卷
探索思考：伟大的数学家高斯在上学读书时曾经研究过这样一个问题：1+2+3+…+10=？
经过研究，这个问题的一般性结论是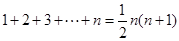：,其中n是正整数。现在，我们来研究一个类似的问题：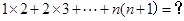
观察下面三个特殊的等式：
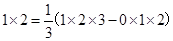
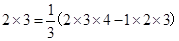
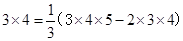
将这三个等式的两边相加，可以得到。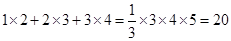
读完这段材料，请你计算下列各题：
（1）；
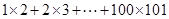（2）；
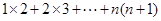（3）．
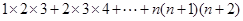粤公网安备 44130202000953号