如图,现有一个以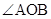 为圆心角、湖岸
为圆心角、湖岸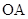 与
与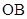 为半径的扇形湖面
为半径的扇形湖面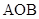 .现欲在弧
.现欲在弧 上取不同于
上取不同于 ,
,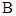 的点
的点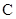 ,用渔网沿着弧
,用渔网沿着弧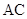 (弧
(弧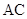 在扇形
在扇形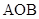 的弧
的弧 上)、半径
上)、半径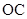 和线段
和线段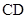 (其中
(其中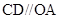 ),在该扇形湖面内隔出两个养殖区域—养殖区域I和养殖区域II.若
),在该扇形湖面内隔出两个养殖区域—养殖区域I和养殖区域II.若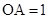
 ,
,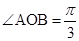 ,
,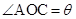 .
.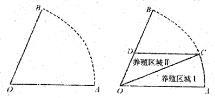
(1)用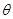 表示
表示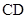 的长度;
的长度;
(2)求所需渔网长度(即图中弧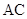 、半径
、半径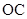 和线段
和线段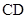 长度之和)的取值范围.
长度之和)的取值范围.
相关知识点
推荐套卷
如图,现有一个以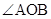 为圆心角、湖岸
为圆心角、湖岸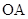 与
与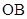 为半径的扇形湖面
为半径的扇形湖面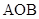 .现欲在弧
.现欲在弧 上取不同于
上取不同于 ,
,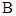 的点
的点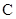 ,用渔网沿着弧
,用渔网沿着弧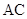 (弧
(弧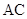 在扇形
在扇形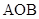 的弧
的弧 上)、半径
上)、半径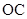 和线段
和线段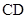 (其中
(其中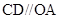 ),在该扇形湖面内隔出两个养殖区域—养殖区域I和养殖区域II.若
),在该扇形湖面内隔出两个养殖区域—养殖区域I和养殖区域II.若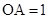
 ,
,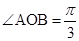 ,
,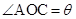 .
.
(1)用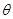 表示
表示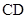 的长度;
的长度;
(2)求所需渔网长度(即图中弧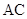 、半径
、半径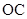 和线段
和线段 长度之和)的取值范围.
长度之和)的取值范围.