己知圆 ,及
,及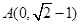 ,
, :
:
①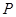 是
是 轴上动点,当
轴上动点,当 最大时,
最大时,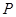 点坐标为
点坐标为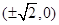
②过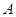 任作一条直线,与圆
任作一条直线,与圆 交于
交于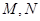 ,则
,则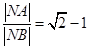
③过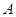 任作一条直线,与圆
任作一条直线,与圆 交于
交于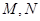 ,则
,则 成立
成立
④任作一条直线与圆 交于
交于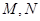 ,则仍有
,则仍有
上述说法正确的是 .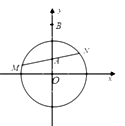
相关知识点
推荐套卷
己知圆 ,及
,及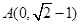 ,
, :
:
①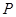 是
是 轴上动点,当
轴上动点,当 最大时,
最大时,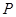 点坐标为
点坐标为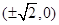
②过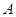 任作一条直线,与圆
任作一条直线,与圆 交于
交于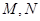 ,则
,则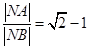
③过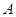 任作一条直线,与圆
任作一条直线,与圆 交于
交于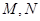 ,则
,则 成立
成立
④任作一条直线与圆 交于
交于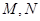 ,则仍有
,则仍有
上述说法正确的是 .