如图，AB为⊙O的直径，D、T是圆上的两点，且AT平分∠BAD，过点T作AD的延长线的垂线PQ，垂足为C．
（1）求证：PQ是⊙O的切线；
（2）已知⊙O的半径为2，若过点O作OE⊥AD，垂足为E，OE=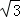 
，求弦AD的长．
,
其中
三角形。
相关知识点
推荐套卷
如图，AB为⊙O的直径，D、T是圆上的两点，且AT平分∠BAD，过点T作AD的延长线的垂线PQ，垂足为C．
（1）求证：PQ是⊙O的切线；
（2）已知⊙O的半径为2，若过点O作OE⊥AD，垂足为E，OE= 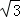，求弦AD的长．
粤公网安备 44130202000953号