(本小题满分12分)为了更好的了解某校高三学生期中考试的数学成绩情况,从所有高三学生中抽取40名学生,将他们的数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图.
(1)若该校高三年级有1800人,试估计这次考试的数学成绩不低于60分的人数及60分以上的学生的平均分;
(2)若从[40,50)与[90,100]这两个分数段内的学生中随机选取两名学生,求这两名学生成绩之差的绝对值不大于10的概率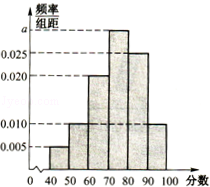
推荐套卷

 ,如图所示。
,如图所示。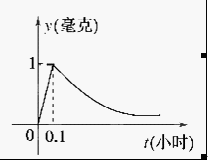
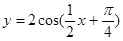

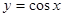 图象经过怎样的变换可以得到
图象经过怎样的变换可以得到 (
( x∈R).
x∈R). ,求
,求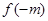 的值;
的值;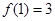 ,求
,求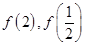 的值。
的值。 求
求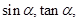
 粤公网安备 44130202000953号
粤公网安备 44130202000953号