已知函数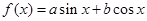 (其中
(其中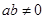 ),且对任意
),且对任意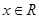 ,有
,有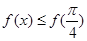 ,给出以下命题:①
,给出以下命题:①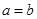 ;②
;②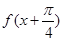 为偶函数;③函数
为偶函数;③函数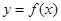 的图象关于点
的图象关于点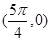 对称;④
对称;④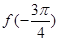 是函数
是函数 的最小值;⑤函数
的最小值;⑤函数 在
在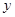 轴右侧的图象与直线
轴右侧的图象与直线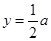 的交点按横坐标从小到依次为
的交点按横坐标从小到依次为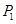 ,
,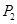 ,
,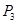 ,
,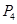 ,…,则
,…,则 .
.
其中正确命题的序号是 .(将所有正确命题的序号都填上)
相关知识点
推荐套卷
已知函数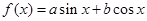 (其中
(其中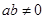 ),且对任意
),且对任意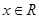 ,有
,有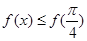 ,给出以下命题:①
,给出以下命题:①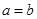 ;②
;②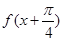 为偶函数;③函数
为偶函数;③函数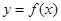 的图象关于点
的图象关于点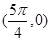 对称;④
对称;④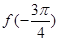 是函数
是函数 的最小值;⑤函数
的最小值;⑤函数 在
在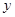 轴右侧的图象与直线
轴右侧的图象与直线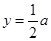 的交点按横坐标从小到依次为
的交点按横坐标从小到依次为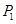 ,
,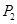 ,
,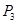 ,
,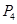 ,…,则
,…,则 .
.
其中正确命题的序号是 .(将所有正确命题的序号都填上)