已知f（x）＝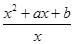
，x∈（0，＋∞）．
（1）若b≥1，求证：函数f（x）在（0,1）上是减函数；
（2）是否存在实数a，b，使f（x）同时满足下列两个条件：
①在（0,1）上是减函数，（1，＋∞）上是增函数；
②f（x）的最小值是3．若存在，求出a，b的值；若不存在，请说明理由．
>3
的定义域为R，求实数m的取值范围
．
；
．相关知识点
推荐套卷
已知f（x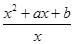）＝，x∈（0，＋∞）．
（1）若b≥1，求证：函数f（x）在（0,1）上是减函数；
（2）是否存在实数a，b，使f（x）同时满足下列两个条件：
①在（0,1）上是减函数，（1，＋∞）上是增函数；
②f（x）的最小值是3．若存在，求出a，b的值；若不存在，请说明理由．
粤公网安备 44130202000953号