（本小题满分12分）函数
是定义在
上的奇函数，且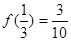
．
（1）求实数
，并确定函数
的解析式；
（2）用定义证明在
上是增函数；
（3）写出的单调减区间，并判断有无最大值或最小值？如有，写出最大值或最小值．（本小问不需说明理由）
互相垂直，求
的值。
对任意的
恒成立，求k的取值范围。
的通项公式；
与
的交点且垂直于直线
的直线方程。
求
的最大值。
B
，C
三点，求D点坐
标，使
且
平行
。相关知识点
推荐套卷
（本小题满分12分）函数是定义在上的奇函数，且．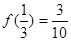
（1）求实数，并确定函数的解析式；
（2）用定义证明在上是增函数；
（3）写出的单调减区间，并判断有无最大值或最小值？如有，写出最大值或最小值．（本小问不需说明理由）
粤公网安备 44130202000953号