在梯形ABCD中，AD∥BC，∠D=90°，以AB为直径作⊙O．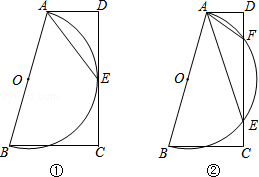
（1）如图①，⊙O与DC相切于点E，
①求证：∠BAE=∠DAE；②若AB=6，求AD+BC的值．
（2）如图②，⊙O与DC交于点E、F．
①图中哪一个角与∠BAE相等？为什么？②试探究线段DF与CE的数量关系，并说明理由．
相关试题
推荐套卷
在梯形ABCD中，AD∥BC，∠D=90°，以AB为直径作⊙O．
（1）如图①，⊙O与DC相切于点E，
①求证：∠BAE=∠DAE；②若AB=6，求AD+BC的值．
（2）如图②，⊙O与DC交于点E、F．
①图中哪一个角与∠BAE相等？为什么？②试探究线段DF与CE的数量关系，并说明理由．
粤公网安备 44130202000953号