如图，已知直线l1∥l2，直线l3和直线l1、l2交于C、D两点，点P在直线CD上.
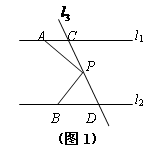
（1）试写出图1中∠APB、∠PAC、∠PBD之间的关系，并说明理由；
（2）如果P点在C、D之间运动时，∠APB，∠PAC，∠PBD之间的关系会发生变化吗？
答： .（填发生或不发生）；
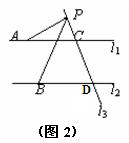
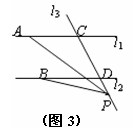
（3）若点P在C、D两点的外侧运动时（P点与点C、D不重合，如图2、图3），试分别写出∠APB，∠PAC，∠PBD之间的关系，并说明理由.
相关试题
+
+
－
配制某种饮料需要甲、乙两种原料，已知这两种原料的维生素C含量以及价格如下表：
（1）配制某种饮料用去甲种原料x千克，乙种原料y千克，求这种饮料中维生素C的含量及配制这种饮料所花的费用；
（2）若x=10，y =15，求此时维生素C的含量及其花费.
＋xy＋y
，求（a＋b）
的值.
粤公网安备 44130202000953号