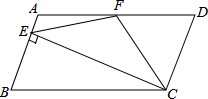
如图，在▱ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论中一定成立的是 ．（把所有正确结论的序号都填在横线上）
①∠DCF=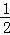
∠BCD；②EF=CF；③S△BEC=2S△CEF；④∠DFE=3∠AEF．
变为
的形式，则
=________
=__________________
相关知识点
推荐套卷
如图，在▱ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论中一定成立的是 ．（把所有正确结论的序号都填在横线上）
①∠DCF=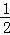∠BCD；②EF=CF；③S△BEC=2S△CEF；④∠DFE=3∠AEF．
粤公网安备 44130202000953号