如图,在平面直角坐标系xOy中,点A 在直线
在直线 上,AB∥y轴,且点B的纵坐标为1,双曲线
上,AB∥y轴,且点B的纵坐标为1,双曲线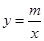 经过点B.
经过点B.
(1)求a的值及双曲线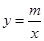 的解析式;
的解析式;
(2)经过点B的直线与双曲线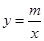 的另一个交点为点C,且△ABC的面积为
的另一个交点为点C,且△ABC的面积为 .
.
①求直线BC的解析式;
②过点B作BD∥x轴交直线 于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
相关知识点
推荐套卷
如图,在平面直角坐标系xOy中,点A 在直线
在直线 上,AB∥y轴,且点B的纵坐标为1,双曲线
上,AB∥y轴,且点B的纵坐标为1,双曲线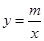 经过点B.
经过点B.
(1)求a的值及双曲线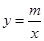 的解析式;
的解析式;
(2)经过点B的直线与双曲线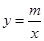 的另一个交点为点C,且△ABC的面积为
的另一个交点为点C,且△ABC的面积为 .
.
①求直线BC的解析式;
②过点B作BD∥x轴交直线 于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.