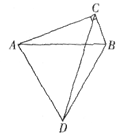
如图，以线段AB为边分别作直角三角形ABC和等边三角形ABD，其中∠ACB=90°.连接CD，当CD的长度最大时，此时∠CAB的大小是（ ）
| A．75° | B．45° |
| C．30° | D．15° |
相关试题
上，则k的值是（ ）
中，自变量x的取值范围是（ ）相关知识点
推荐套卷
如图，以线段AB为边分别作直角三角形ABC和等边三角形ABD，其中∠ACB=90°.连接CD，当CD的长度最大时，此时∠CAB的大小是（ ）
| A．75° | B．45° |
| C．30° | D．15° |
粤公网安备 44130202000953号