某校高三年级一次数学考试之后，为了解学生的数学学习情况，随机抽取n名学生的数学成绩，制成如表所示的频率分布表．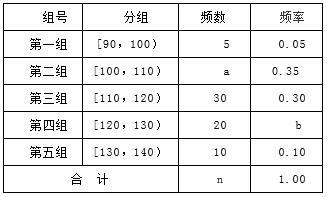
（1）求a，b，n的值；
（2）若从第三、四、五组中用分层抽样方法抽取6名学生，并在这6名学生中随机抽取2名与张老师面谈，求第三组中至少有1名学生与张老师面谈的概率．
相关试题
．
的奇偶性，并证明；
的
的取值范围．
；
．
，
．
，求
的取值范围；
，求
，直线
是圆的一条切线，且
与椭圆
交于不同的两点
．
与
的关系；
的长为
，求直线
及圆
．
过点
且被圆
截得的线段
长为
，求直线推荐套卷
某校高三年级一次数学考试之后，为了解学生的数学学习情况，随机抽取n名学生的数学成绩，制成如表所示的频率分布表．
（1）求a，b，n的值；
（2）若从第三、四、五组中用分层抽样方法抽取6名学生，并在这6名学生中随机抽取2名与张老师面谈，求第三组中至少有1名学生与张老师面谈的概率．
粤公网安备 44130202000953号