（本小题满分12分）山东省济南市为了共享优质教育资源，实现名师交流，甲、乙两校各有
名教师报名交流，其中甲校
男
女，乙校男女．
（Ⅰ）若从甲校和乙校报名的教师中各任选名，写出所有可能的结果，并求选出的名教师性别相同的概率；
（Ⅱ）若从报名的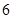
名教师中任选名，写出所有可能的结果，并求选出的名教师来自同一学校的概率．
表示两条直线,求m的值
+(x-1)0 ; 
);(3)y=f(
; (4)y=f(x+a)+f(x-a).推荐套卷
（本小题满分12分）山东省济南市为了共享优质教育资源，实现名师交流，甲、乙两校各有名教师报名交流，其中甲校男女，乙校男女．
（Ⅰ）若从甲校和乙校报名的教师中各任选名，写出所有可能的结果，并求选出的名教师性别相同的概率；
（Ⅱ）若从报名的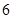名教师中任选名，写出所有可能的结果，并求选出的名教师来自同一学校的概率．
粤公网安备 44130202000953号