如图,一扇窗户垂直打开,即OM⊥OP,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端在OP上滑动,将窗户OM按图示方向向内旋转35°到达ON位置,此时,点A、C的对应位置分别是点B、D.测量出∠ODB为25°,点D到点O的距离为30cm.
(1)求B点到OP的距离;
(2)求滑动支架的长.
(结果精确到1cm.参考数据:sin25°≈0.42,cos25°≈0.91,tan25°≈0.47,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
相关知识点
推荐套卷
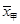 =9环,方差
=9环,方差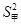 =
=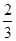 .
.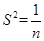 [(x1-
[(x1-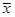 )2+(x2-
)2+(x2-
 粤公网安备 44130202000953号
粤公网安备 44130202000953号