推理填空，如图，已知∠A=∠F，∠C=∠D，试说明BD∥CE．
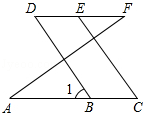
解：∵∠A=∠F（ ），
∴AC∥DF（ ），
∴∠D=∠1（ ），
又∵∠C=∠D（ ），
∴∠1=∠C（ ），
∴BD∥CE（ ）．
推理填空，如图，已知∠A=∠F，∠C=∠D，试说明BD∥CE．
解：∵∠A=∠F（ ），
∴AC∥DF（ ），
∴∠D=∠1（ ），
又∵∠C=∠D（ ），
∴∠1=∠C（ ），
∴BD∥CE（ ）．
，那么a －b =________
+9
的和等于3
与
是同类项，则
=.
粤公网安备 44130202000953号