某岛是我国南海上的一个岛屿，小明据此构造出该岛的一个数学模型如图甲所示，其中∠B=90°，AB=100
千米，∠BAC=30°，请据此解答如下问题：
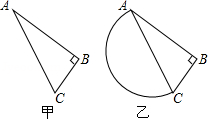
（1）求该岛的周长和面积（结果保留整数，参考数据
≈1.414，≈1.73，
≈2.45）；
（2）国家为了建设的需要，在原有岛屿基础上沿海岸线AC向海洋填海，扩充岛屿的面积（如图乙），填成一个以AC为直径的半圆，点D在这个半圆上，求当△ACD的面积最大时，△ACD另外两条边的边长．
相关试题
，BD平分
，且
，
．求AB的值．
在开展“学雷锋社会实践”活动中，某校为了解全校1200名学生参加活动的情况，随机调查了50名学生每人参加活动的次数，并根据数据绘成条形统计图如下：
（1）求这50个样本数据的平均数、众数、中位数；
（2）根据样本数据，估算该校1200名学生共参加了多少次活动？
如图，平行四边形ABCD中，E是CD的延长线上一点，BE与AD交于点F，DE=
CD．
（1）求证：△ABF∽△CEB；
（2）若△DEF的面积为2，求平行四边形的面积．
，求AB．
与反比例函数
的图象交于A，B两点．求A，B两点的坐标．
相关知识点
推荐套卷
粤公网安备 44130202000953号