已知边长为4的正方形ABCD,顶点A与坐标原点重合,一反比例函数图象过顶点C,动点P以每秒1个单位速度从点A出发沿AB方向运动,动点Q同时以每秒4个单位速度从D点出发沿正方形的边DC﹣CB﹣BA方向顺时针折线运动,当点P与点Q相遇时停止运动,设点P的运动时间为t.
(1)求出该反比例函数解析式;
(2)连接PD,当以点Q和正方形的某两个顶点组成的三角形和△PAD全等时,求点Q的坐标;
(3)用含t的代数式表示以点Q、P、D为顶点的三角形的面积s,并指出相应t的取值.
相关知识点
推荐套卷
 是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.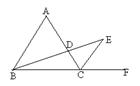
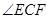 的度数等于__________°;
的度数等于__________°; 中,AB=AC=
中,AB=AC=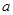 ,
,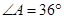 ,BD平分
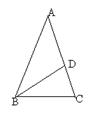
,BD平分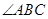 .
.
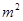 .问道路应为多少宽?
.问道路应为多少宽?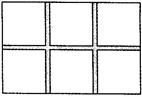
 的方程
的方程 .
. 时,该方程的根是;
时,该方程的根是; 时,该方程有两个不相等的实数根吗?并说明理由.
时,该方程有两个不相等的实数根吗?并说明理由. .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号