如图所示,已知点C(-3,m),点D(m-3,0).直线CD交y轴于点A.作CE与X轴垂直,垂足为E,以点B(-1,0)为顶点的抛物线恰好经过点A、C.

(1)则∠CDE= ;
(2)求抛物线对应的函数关系式;
(3)设P(x,y)为抛物线上一点(其中-3<x<1-或-1<x<1,连结BP并延长交直线CE于点N,记N点的纵坐标为yN,连结CP并延长交X轴于点M.
①试证明:EM•(EC+yN)为定值;
②试判断EM+EC+yN是否有最小值,并说明理由
相关知识点
推荐套卷
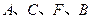 在同一直线上,
在同一直线上,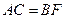 ,
,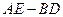 ,且
,且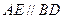 。求证:
。求证: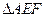 与
与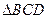 全等。
全等。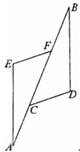
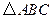 是格点三角形.在建立平面直角坐标系后,点
是格点三角形.在建立平面直角坐标系后,点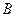 的坐标为(
的坐标为(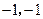 ).
).
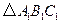 ,画出
,画出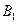 的坐标
的坐标 ;
;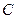 按顺时针方向旋转
按顺时针方向旋转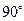 后得到
后得到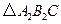 ,画出
,画出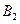 的坐标;
的坐标;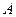 为位似中心放大,使放大前后对应边长的比为
为位似中心放大,使放大前后对应边长的比为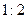 ,画出
,画出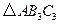 的图形.
的图形.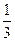 .
.
 ,四边形A′B′C′D′和四边形A″B″C″D″位似,位似比
,四边形A′B′C′D′和四边形A″B″C″D″位似,位似比 .四边形A″B″C″D″和四边形ABCD是位似图形吗?位似比是多少?
.四边形A″B″C″D″和四边形ABCD是位似图形吗?位似比是多少?
 和
和 .
.
 为位似中心,把
为位似中心,把 .
. ,
, ,
, 的位置.
的位置. 粤公网安备 44130202000953号
粤公网安备 44130202000953号