海水受日月的引力,在一定的时候发生涨落的现象叫潮,一般地,早潮叫潮,晚潮叫汐. 在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋. 下面是某港口在某季节每天的时间与水深关系表:
时刻
|
2:00
|
5:00
|
8:00
|
11:00
|
14:00
|
17:00
|
20:00
|
23:00
|
水深(米)
|
7.5
|
5.0
|
2.5
|
5.0
|
7.5
|
5.0
|
2.5
|
5.0
|
经长期观测,这个港口的水深与时间的关系,可近似用函数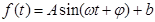
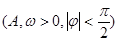 来描述.
来描述.
(1)根据以上数据,求出函数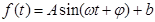 的表达式;
的表达式;
(2)一条货船的吃水深度(船底与水面的距离)为4.25米,安全条例规定至少要有2米的安全间隙(船底与洋底的距离),该船在一天内(0:00~24:00)何时能进入港口?在港口能停留多久?