如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC于D．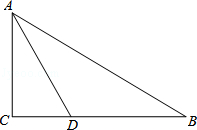
（1）动手操作：利用尺规作⊙O，使⊙O经过点A、D，且圆心O在AB上；并标出⊙O与AB的另一个交点E（保留作图痕迹，不写作法）；
（2）综合应用：在你所作的图中，
①判断直线BC与⊙O的位置关系，并说明理由；
②若AB=6，BD=2
，求线段BD、BE与劣弧
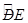所围成的图形面积（结果保留根号和π）．
相关试题
．
．
相关知识点
推荐套卷
如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC于D．
（1）动手操作：利用尺规作⊙O，使⊙O经过点A、D，且圆心O在AB上；并标出⊙O与AB的另一个交点E（保留作图痕迹，不写作法）；
（2）综合应用：在你所作的图中，
①判断直线BC与⊙O的位置关系，并说明理由；
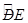②若AB=6，BD=2，求线段BD、BE与劣弧所围成的图形面积（结果保留根号和π）．
粤公网安备 44130202000953号