如图,抛物线y=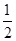 x2+bx+c经过A(-1,0),C(2,-3)两点,与y轴交于点D,与x轴交于另一点B.
x2+bx+c经过A(-1,0),C(2,-3)两点,与y轴交于点D,与x轴交于另一点B.
(1)求此抛物线的解析式及顶点坐标;
(2)若将此抛物线平移,使其顶点为点D,需如何平移?写出平移后抛物线的解析式;
(3)过点P(m,0)作x轴的垂线(1≤m≤2),分别交平移前后的抛物线于点E,F,交直线OC于点G,求证:PF=EG.
相关知识点
推荐套卷
如图,抛物线y=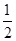 x2+bx+c经过A(-1,0),C(2,-3)两点,与y轴交于点D,与x轴交于另一点B.
x2+bx+c经过A(-1,0),C(2,-3)两点,与y轴交于点D,与x轴交于另一点B.
(1)求此抛物线的解析式及顶点坐标;
(2)若将此抛物线平移,使其顶点为点D,需如何平移?写出平移后抛物线的解析式;
(3)过点P(m,0)作x轴的垂线(1≤m≤2),分别交平移前后的抛物线于点E,F,交直线OC于点G,求证:PF=EG.