如图，抛物线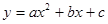
（
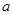≠0）与
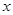轴交于A（-4，0），B（2，0），与
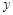轴交与点C（0，2）．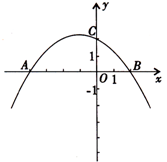
（1）求抛物线的解析式；
（2）若点D为该抛物线上的一个动点，且在直线AC上方，当以A，C，D为顶点的三角形面积最大时，求点D的坐标及此时三角形的面积；（解题用图见答题卡）
（3）以AB为直径作⊙M，直线经过点E（-1，-5），并且与⊙M相切，求该直线的解析式．（解题用图见答题卡）
相关试题
，其中
．
相关知识点
推荐套卷
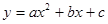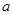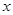如图，抛物线（≠0）与轴交于A（-4，0），B（2，0），与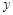轴交与点C（0，2）．
（1）求抛物线的解析式；
（2）若点D为该抛物线上的一个动点，且在直线AC上方，当以A，C，D为顶点的三角形面积最大时，求点D的坐标及此时三角形的面积；（解题用图见答题卡）
（3）以AB为直径作⊙M，直线经过点E（-1，-5），并且与⊙M相切，求该直线的解析式．（解题用图见答题卡）
粤公网安备 44130202000953号