在平面直角坐标系中，点
的坐标是（0，3），点
在
轴上，将
绕点
逆时针旋转90°得到
，点
、
的对应点分别是点
、
．
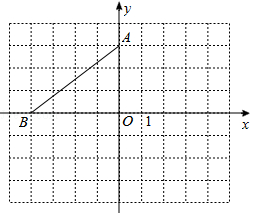
（1）若点
的坐标是
，请在图中画出
，并写出点
、
的坐标．
（2）当点
落在
轴的上方时，试写出一个符合条件的点
的坐标．
相关试题
≤
． 
．如图1，在平面直角坐标系中，点A的坐标为(1,2)，点B的坐标为（3，1），二次函数y=x2的图象记为抛物线l1．
（1）平移抛物线l1，使平移后的抛物线过点A，但不过点B，写出平移后的一个抛物线的函数表达式（任写一个即可）；
（2）平移抛物线l1，使平移后的抛物线过A，B两点，记为抛物线l2，如图2，求抛物线l2的函数表达式；
（3）设抛物线l2的顶点为C，K为y轴上一点．若S△ABK=S△ABC，求点K的坐标；
（4）请在图3上用尺规作图的方式探究抛物线l2上是否存在点P，使△ABP为等腰三角形．若存在，请判断点P共有几个可能的位置（保留作图痕迹）；若不存在，请说明理由．
相关知识点
推荐套卷
粤公网安备 44130202000953号