某学校为了解七年级男生体质健康情况，随机抽取若干名男生进行测试，测试结果分为优秀、良好、合格、不合格四个等级，统计整理数据并绘制图1、图2两幅不完整的统计图，请根据图中信息回答下列问题：
（1）本次接收随机抽样调查的男生人数为 人，扇形统计图中“良好”所对应的圆心角的度数为 ；
（2）补全条形统计图中“优秀”的空缺部分；
（3）若该校七年级共有男生480人，请估计全年级男生体质健康状况达到“良好”的人数．
相关试题
要在规定的日期内加工一批机器零件，如果甲单独做，刚好在规定日期内完成，乙单独做则要超过3天．现在甲、乙两人合作2天后，再由乙单独做，正好按期完成，问规定日期是多少天？
如图：已知在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E，F．
（1）求证：△BED≌△CFD；
（2）若∠A=90°，求证：四边形DFAE是正方形．
“最美女教师”张丽莉，为抢救两名学生，以致双腿高位截肢，社会各界纷纷为她捐款，我市某中学九年级一班全体同学参加了捐款活动，该班同学捐款情况的部分统计图如图所示：
（1）求该班的总人数；
（2）将条形图补充完整，并写出捐款总额的众数；
（3）该班平均每人捐款多少元？
﹣
）÷
，然后从不等式组
的解集中选取一个你认为合适的整数作为a的值代入求值．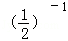
+
+
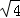
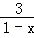=1．相关知识点
推荐套卷
粤公网安备 44130202000953号