如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.
(1)当动点P与点B重合时,若点B的坐标是(2,1),求PA的长.
(2)当动点P在线段OB的延长线上时,若点A的纵坐标与点B的横坐标相等,求PA:PC的值.
(3)当动点P在直线OB上时,点D是直线OB与直线CA的交点,点E是直线CP与y轴的交点,若∠ACE=∠AEC,PD=2OD,求PA:PC的值.
相关知识点
推荐套卷
 地区
地区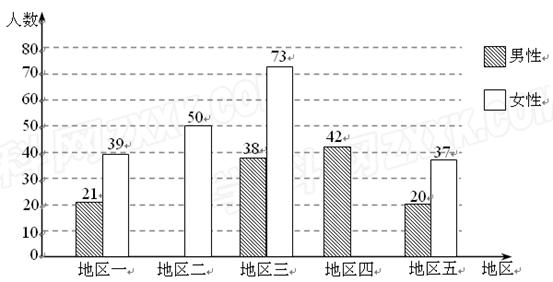
 2015年该市100周岁以上的老人将比2008年2月的统计数增加100人,请你估算2015年地区一增加100周岁以上的男性老人多少人?
2015年该市100周岁以上的老人将比2008年2月的统计数增加100人,请你估算2015年地区一增加100周岁以上的男性老人多少人?




 粤公网安备 44130202000953号
粤公网安备 44130202000953号