如图,已知直线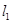 ∥
∥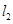 ,
,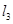 、
、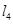 和
和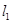 、
、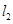 分别交于点
分别交于点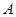 、
、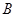 、
、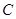 、
、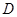 ,点
,点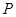 在直线
在直线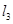 或
或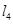 上且不与点
上且不与点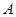 、
、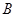 、
、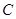 、
、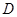 重合.记
重合.记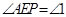 ,
,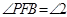 ,
,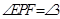 .
.
(1)若点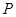 在图(1)位置时,求证:
在图(1)位置时,求证: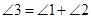 ;
;
(2)若点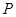 在图(2)位置时,请直接写出
在图(2)位置时,请直接写出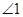 、
、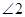 、
、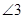 之间的关系;
之间的关系;
(3)若点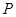 在图(3)位置时,写出
在图(3)位置时,写出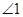 、
、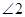 、
、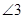 之间的关系并给予证明.
之间的关系并给予证明.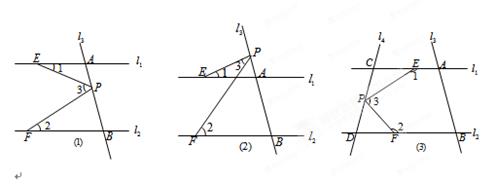
如图,已知直线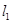 ∥
∥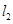 ,
,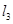 、
、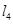 和
和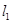 、
、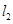 分别交于点
分别交于点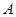 、
、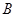 、
、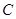 、
、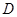 ,点
,点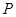 在直线
在直线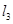 或
或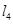 上且不与点
上且不与点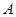 、
、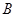 、
、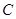 、
、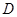 重合.记
重合.记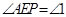 ,
,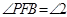 ,
,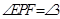 .
.
(1)若点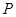 在图(1)位置时,求证:
在图(1)位置时,求证: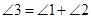 ;
;
(2)若点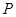 在图(2)位置时,请直接写出
在图(2)位置时,请直接写出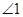 、
、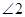 、
、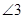 之间的关系;
之间的关系;
(3)若点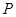 在图(3)位置时,写出
在图(3)位置时,写出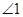 、
、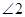 、
、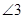 之间的关系并给予证明.
之间的关系并给予证明.