如图，已知：在平行四边形ABCD中，点E、F、G、H分别在边AB、BC、CD、DA上，AE=CG，AH=CF，且EG平分∠HEF．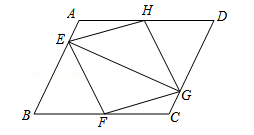
求证：（1）△AEH≌△CGF；
（2）四边形EFGH是菱形．
相关试题
相关知识点
推荐套卷
如图，已知：在平行四边形ABCD中，点E、F、G、H分别在边AB、BC、CD、DA上，AE=CG，AH=CF，且EG平分∠HEF．
求证：（1）△AEH≌△CGF；
（2）四边形EFGH是菱形．
粤公网安备 44130202000953号