在不透明的袋子中有四张标着数字1,2,3,4 的卡片,这些卡片除数字外都相同.甲同学按照一定的规则抽出两张卡片,并把卡片上的数字相加.如图是他所画的树状图的一部分.
(1)由如图分析,甲同学的游戏规则是:从袋子中随机抽出一张卡片后 (填“放回”或“不放回”),再随机抽出一张卡片;
(2)帮甲同学完成树状图;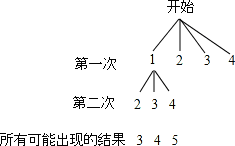
(3)求甲同学两次抽到的数字之和为偶数的概率.
相关知识点
推荐套卷
在不透明的袋子中有四张标着数字1,2,3,4 的卡片,这些卡片除数字外都相同.甲同学按照一定的规则抽出两张卡片,并把卡片上的数字相加.如图是他所画的树状图的一部分.
(1)由如图分析,甲同学的游戏规则是:从袋子中随机抽出一张卡片后 (填“放回”或“不放回”),再随机抽出一张卡片;
(2)帮甲同学完成树状图;
(3)求甲同学两次抽到的数字之和为偶数的概率.