射线QN与等边△ABC的两边AB，BC分别交于点M，N，且AC∥QN，AM=MB=2cm，QM=4cm．动点P从点Q出发，沿射线QN以每秒1cm的速度向右移动，经过t秒，以点P为圆心，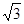
cm为半径的圆与△ABC的边相切（切点在边上），请写出t可取的一切值_________。（单位：秒）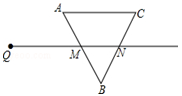
相关试题
,则由此
为三边的三角形面积为。
相关知识点
推荐套卷
射线QN与等边△ABC的两边AB，BC分别交于点M，N，且AC∥QN，AM=MB=2cm，QM=4cm．动点P从点Q出发，沿射线QN以每秒1cm的速度向右移动，经过t秒，以点P为圆心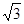，cm为半径的圆与△ABC的边相切（切点在边上），请写出t可取的一切值_________。（单位：秒）
粤公网安备 44130202000953号