在平面直角坐标系 中,点A(-3,0),B(3,0),动点P满足
中,点A(-3,0),B(3,0),动点P满足
(1)若点P的轨迹为曲线C,求此曲线的方程;
(2)若点Q在直线l1:x+y+3=0上,直线l2经过点Q且与曲线C只有一个公共点M,求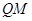 的最小值.
的最小值.
(3)动圆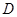 的半径为
的半径为 ,圆心在在直线
,圆心在在直线 上,若圆
上,若圆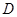 上存在点
上存在点 ,使得
,使得 ,求圆心
,求圆心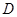 的纵坐标
的纵坐标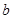 的取值范围.
的取值范围.
相关知识点
推荐套卷
在平面直角坐标系 中,点A(-3,0),B(3,0),动点P满足
中,点A(-3,0),B(3,0),动点P满足
(1)若点P的轨迹为曲线C,求此曲线的方程;
(2)若点Q在直线l1:x+y+3=0上,直线l2经过点Q且与曲线C只有一个公共点M,求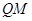 的最小值.
的最小值.
(3)动圆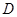 的半径为
的半径为 ,圆心在在直线
,圆心在在直线 上,若圆
上,若圆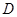 上存在点
上存在点 ,使得
,使得 ,求圆心
,求圆心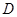 的纵坐标
的纵坐标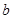 的取值范围.
的取值范围.