已知椭圆
的中心为
，右顶点为
，在线段
上任意选定一点
，过点
作与
轴垂直的直线交
于
两点.
（Ⅰ）若椭圆的长半轴为2，离心率
，
（ⅰ）求椭圆的标准方程；
（ⅱ）若
，点
在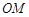
的延长线上，且
成等比数列，试证明直线
与相切；
（Ⅱ）试猜想过椭圆
上一点
的切线方程的一种方法，再加以证明.
＝
的最大值；
，求证：
对于一切
都成立？
,从集合
中各取2个元素组成没有重复数字的四位数.
与直线
所围成图形的面积。
的图像与直线
相切于点（1，－11）
的值；
的单调性。推荐套卷
已知椭圆的中心为，右顶点为，在线段上任意选定一点，过点作与轴垂直的直线交于两点.
（Ⅰ）若椭圆的长半轴为2，离心率，
（ⅰ）求椭圆的标准方程；
（ⅱ）若，点在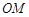的延长线上，且成等比数列，试证明直线与相切；
（Ⅱ）试猜想过椭圆上一点的切线方程的一种方法，再加以证明.
粤公网安备 44130202000953号