如图1所示,在Rt△ABC中,∠ACB=90°,点D为边BC上任意一点,以直线AD为对称轴,作Rt△ABC的轴对称图形Rt△AEF,点M、点N、点P、点Q分别为AB、BC、EF、EA的中点.
(1)求证:MN=PQ;
(2)如图2,当BD=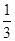 BC时,判断点M、点N、点P、点Q围成的四边形的形状,并说明理由;
BC时,判断点M、点N、点P、点Q围成的四边形的形状,并说明理由;
(3)若BC=6,请你直接写出当①BD=0;②BD=3;③BD=2;④BD=6时,点M、点N、点P、点Q围成的图形的形状.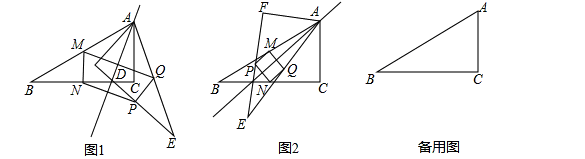
相关知识点
推荐套卷
 与x轴交于A、C两点,与y轴交于B点,与直线y=kx+b交于A、D两点.
与x轴交于A、C两点,与y轴交于B点,与直线y=kx+b交于A、D两点.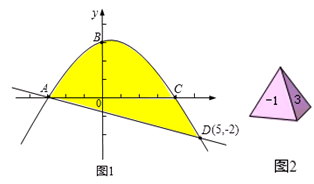
 为直径的⊙
为直径的⊙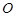 交线段
交线段 于点
于点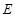 ,点
,点 是弧AE的中点,
是弧AE的中点,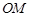 交
交 ,
, °,
°, ,
, .
.
 =°;
=°;

 |
| .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号