某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本 (单位:元)、销售价
(单位:元)、销售价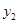 (单位:元)与产量x(单位:kg)之间的函数关系.
(单位:元)与产量x(单位:kg)之间的函数关系.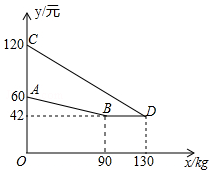
(1)请解释图中点D的横坐标、纵坐标的实际意义;
(2)求线段AB所表示的 与x之间的函数表达式;
与x之间的函数表达式;
(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?
推荐套卷
某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本 (单位:元)、销售价
(单位:元)、销售价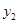 (单位:元)与产量x(单位:kg)之间的函数关系.
(单位:元)与产量x(单位:kg)之间的函数关系.
(1)请解释图中点D的横坐标、纵坐标的实际意义;
(2)求线段AB所表示的 与x之间的函数表达式;
与x之间的函数表达式;
(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?