（本题10分）某医药研究所开发一种新药．在试验药效时发现，如果成人按规定剂量服用，那么服药2h后血液中含药量最高，达到每毫升6μg（1μg＝10－3mg），接着逐步衰减，10h后血液中含药量为每毫升3μg．若每毫升血液中含药量y（μg）随时间x（h）的变化如图所示，则当成人按规定剂量服药后：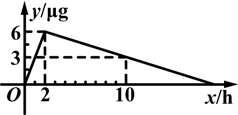
（1）分别求出0≤x≤2和x＞2时，y与x之间的函数解析式；
（2）如果每毫升血液中含药量为4μg或4μg以上时药物对疾病的治疗是有效的，那么这个有效时间是多长？
（本小题满分7分）已知：等边三角形ABC
（1）如图1，P为等边△ABC外一点，且∠
BPC=120°．试猜想线段BP、PC、AP之间的数量关系,并证明
你的猜想；
（2）如图2，P为等边△ABC内一点，且∠APD=120°．求证：PA+PD+PC＞BD
（本小题满分8分）如图，抛物线
（
＞0）与y轴交于点C,与x轴交于A 、B两
点，点 A在点B的左侧，且
．
（1）求此抛物线的解析式；
（2）如果点D是线段AC下方
抛物线上的动点，设D点的横坐标为x，△ACD的面积为S，求S与x的关系式，并求当S最大时点D的坐标；
（3）若点E在x轴上，点P在抛物线上，是否存在以A、C、E、P为顶点的平行四边形？若存在求点P坐标；若不存在，请说明理由．
（本小题满分7分）已知：关于
的一元二次方程
．
（1）若方程有两个不相等的实数根，求
的取值范围；
（2）在（1）的条件下，求证：无论取何值，抛物线y=
总过轴上的一个固定点；
（3）若为正整数，且关于的一元二次方程有两个不相等的整数根，把抛物线y=向右平移4个单位长度，求平移后的抛物线的解析式．
（本小题满分5分）
小明想把一个三角形拼接成面积与它相等的矩形．他先进行了如下部分操作，如图1所示：
①取△ABC的边AB、AC的中点D、E，联结DE；
②过点A作AF⊥DE于点F；
（1）请你帮小明完成图1的操作，把△ABC拼接成面积与它相等的矩形．
（2）若把一个三角形通过类似的操作拼接成一个与原三角形面积相等的正方形，那么原三角形的一边与这边上的高之间的数量关系是________________．
（3）在下面所给的网格中画出符合（2）中条件的三角形，并将其拼接成面积与它相等的正方形
．
__________；
粤公网安备 44130202000953号