【2015高考上海,理20】如图,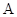 ,
,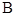 ,
,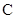 三地有直道相通,
三地有直道相通, 千米,
千米, 千米,
千米, 千米.现甲、乙两警员同时从
千米.现甲、乙两警员同时从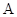 地出发匀速前往
地出发匀速前往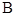 地,经过
地,经过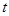 小时,他们之间的距离为
小时,他们之间的距离为 (单位:千米).甲的路线是
(单位:千米).甲的路线是 ,速度为
,速度为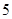 千米/小时,乙的路线是
千米/小时,乙的路线是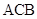 ,速度为
,速度为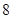 千米/小时.乙到达
千米/小时.乙到达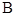 地后原地等待.设
地后原地等待.设 时乙到达
时乙到达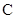 地.
地.
(1)求 与
与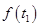 的值;
的值;
(2)已知警员的对讲机的有效通话距离是 千米.当
千米.当 时,求
时,求 的表达式,并判断
的表达式,并判断 在
在 上得最大值是否超过
上得最大值是否超过 ?说明理由.
?说明理由.
推荐套卷
【2015高考上海,理20】如图,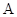 ,
,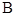 ,
,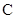 三地有直道相通,
三地有直道相通, 千米,
千米, 千米,
千米, 千米.现甲、乙两警员同时从
千米.现甲、乙两警员同时从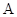 地出发匀速前往
地出发匀速前往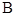 地,经过
地,经过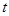 小时,他们之间的距离为
小时,他们之间的距离为 (单位:千米).甲的路线是
(单位:千米).甲的路线是 ,速度为
,速度为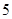 千米/小时,乙的路线是
千米/小时,乙的路线是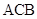 ,速度为
,速度为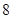 千米/小时.乙到达
千米/小时.乙到达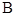 地后原地等待.设
地后原地等待.设 时乙到达
时乙到达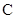 地.
地.
(1)求 与
与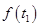 的值;
的值;
(2)已知警员的对讲机的有效通话距离是 千米.当
千米.当 时,求
时,求 的表达式,并判断
的表达式,并判断 在
在 上得最大值是否超过
上得最大值是否超过 ?说明理由.
?说明理由.