实践与操作:如图1是以正方形两顶点为圆心,边长为半径,画两段相等的圆弧而成的轴对称图形,图2是以图1为基本图案经过图形变换拼成的一个中心对称图形.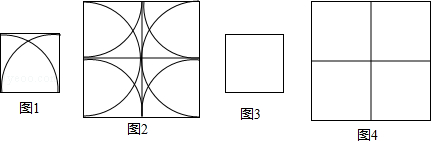
(1)请你仿照图1,用两段相等圆弧(小于或等于半圆),在图3中重新设计一个不同的轴对称图形.
(2)以你在图3中所画的图形为基本图案,经过图形变换在图4中拼成一个中心对称图形.
相关知识点
推荐套卷
实践与操作:如图1是以正方形两顶点为圆心,边长为半径,画两段相等的圆弧而成的轴对称图形,图2是以图1为基本图案经过图形变换拼成的一个中心对称图形.
(1)请你仿照图1,用两段相等圆弧(小于或等于半圆),在图3中重新设计一个不同的轴对称图形.
(2)以你在图3中所画的图形为基本图案,经过图形变换在图4中拼成一个中心对称图形.