云南 年秋季以来遭遇百年一遇的全省性特大旱灾,部分坝塘干涸,小河、小溪断流,更为严重的情况是有的水库已经见底,全省库塘蓄水急剧减少,为确保城乡居民生活用水,有关部门需要对某水库的现存水量进行统计,以下是技术员在测量时的一些数据:水库大坝的横截面是梯形
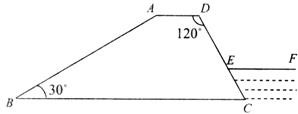
年秋季以来遭遇百年一遇的全省性特大旱灾,部分坝塘干涸,小河、小溪断流,更为严重的情况是有的水库已经见底,全省库塘蓄水急剧减少,为确保城乡居民生活用水,有关部门需要对某水库的现存水量进行统计,以下是技术员在测量时的一些数据:水库大坝的横截面是梯形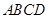 (如图所示),
(如图所示),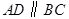 ,
,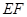 为水面,点
为水面,点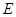 在
在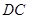 上,测得背水坡
上,测得背水坡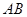 的长为
的长为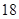 米,倾角
米,倾角 ,迎水坡
,迎水坡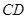 上线段
上线段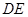 的长为
的长为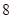 米,
米,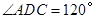 .
.
(1)请你帮技术员算出水的深度(精确到 米,参考数据
米,参考数据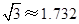 );
);
(2)就水的深度而言,平均每天水位下降必须控制在多少米以内,才能保证现有水量至少能使用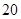 天?(精确到
天?(精确到 米)
米)
相关知识点
推荐套卷
 粤公网安备 44130202000953号
粤公网安备 44130202000953号