学校为统筹安排大课间体育活动,在各班随机选取了一部分学生,分成四类活动:“篮球”、 “羽毛球”、 “乒乓球”、“其他”进行调查,整理收集到的数据,绘制成如下的两幅统计图.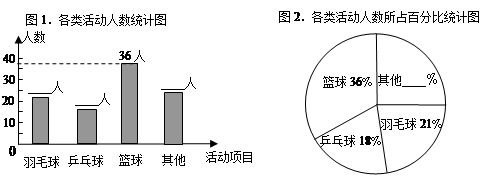
(1)学校采用的调查方式是 ;学校在各班共随机选取了 名学生;
(2)补全统计图中的数据:羽毛球 人、乒乓球 人、其他 人、其他 ﹪;
(3)该校共有1100名学生,请计算喜欢“篮球”的学生人数.
相关知识点
推荐套卷
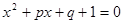 的一根为2.
的一根为2.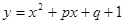 与x轴总有交点。
与x轴总有交点。 =4时,求P点的坐标.
=4时,求P点的坐标. (x>0)交于D点,过点D作DC⊥x轴,垂足为G,连接OD.已知△AOB≌△ACD.
(x>0)交于D点,过点D作DC⊥x轴,垂足为G,连接OD.已知△AOB≌△ACD.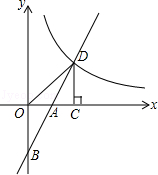
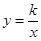 (x>0)的图象和矩形ABCD的第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).
(x>0)的图象和矩形ABCD的第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).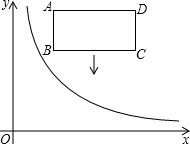
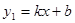 与反比例函数
与反比例函数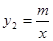 的图象交于A(2,4)、B(﹣4,n)两点.
的图象交于A(2,4)、B(﹣4,n)两点.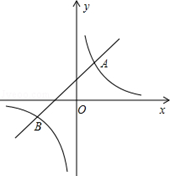
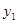 和
和 的解析式;
的解析式; 粤公网安备 44130202000953号
粤公网安备 44130202000953号