已知在Rt△ABC中，∠ACB=90°，现按如下步骤作图：
①分别以A，C为圆心，a为半径（a＞
AC）作弧，两弧分别交于M，N两点；
②过M，N两点作直线MN交AB于点D，交AC于点E；
③将△ADE绕点E顺时针旋转180°，设点D的像为点F．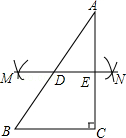
（1）请在图中直线标出点F并连接CF；
（2）求证：四边形BCFD是平行四边形；
（3）当∠B为多少度时，四边形BCFD是菱形．
相关试题
，且点A、B到原点的距离相等，求
的值. 
>20）之间的函数关系式；
，其中
．
（结果化为只含有正指数幂的形式）
推荐套卷
已知在Rt△ABC中，∠ACB=90°，现按如下步骤作图：
①分别以A，C为圆心，a为半径（a＞AC）作弧，两弧分别交于M，N两点；
②过M，N两点作直线MN交AB于点D，交AC于点E；
③将△ADE绕点E顺时针旋转180°，设点D的像为点F．
（1）请在图中直线标出点F并连接CF；
（2）求证：四边形BCFD是平行四边形；
（3）当∠B为多少度时，四边形BCFD是菱形．
粤公网安备 44130202000953号